
 CausaDirecta.com
Investigación y Reconstrucción de Accidentes de Tráfico
CausaDirecta.com
Investigación y Reconstrucción de Accidentes de Tráfico

Cálculos (4)
Cálculo de velocidad a partir de grabaciones de vídeo
Escrito por CausaDirecta
Lo último en el Foro de CausaDirecta.com
| Así ocurrió mi accidente | CALCULO DE LA VELOCIDAD DE MOTO | (7) |
| Luis H > 17/02/2025 | 07:30 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:13 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:12 | |
| Anécdotas | Milionário la calle | (3) |
| MIguelitoalc > 10/01/2025 | 12:27 | |
| Trámites y Reclamaciones | Accidente de moto. | (1) |
| Sègimer > 05/05/2024 | 09:03 | |
| Testigos de accidentes | Se buscan testigos accidente día 23/11/2023 en Valladolid | (2) |
| > 18/04/2024 | 19:07 | |
| Trámites y Reclamaciones | Discriminación en perfumeria Druni | (1) |
| Melior.Mundi > 03/03/2024 | 13:07 | |
| Así ocurrió mi accidente | Desconformidad y dudas en atestado Motocicleta | (1) |
| anteva2 > 24/11/2023 | 11:47 | |
| Punto de Encuentro (Investigación y Reconstrucción) | Documentación sobre la fórmula de Vangi-Cialdai | (1) |
| Jugo > 05/11/2023 | 22:04 | |
| Así ocurrió mi accidente | Dudas culpabilidad accidente, pref. derecha y exceso Velocid | (2) |
| pitutis > 12/10/2023 | 11:19 | |
INVESTIGACIÓN DE ATROPELLOS
FÓRMULA DE LA VELOCIDAD MÍNIMA A LA QUE SE PROYECTA AL PEATÓN
Enviado por: Taker
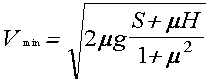
donde:
µ: coeficiente de rozamiento peatón-pavimento.
g: gravedad ( 9,81 m/s²)
S: distancia recorrida por el peatón tras el impacto.
H: Altura a la que queda detenido el peatón tras el impacto. La altura se mide respecto de un valor H cero. Éste puede ser bien el centro de gravedad de la persona,( H cero : 0.95 m), bien la propia calzada.
Si el atropello además se produce en una pendiente habrá que introducir el factor de corrección oportuno. Hay dos posibilidades:
A.-
Corrigiendo el valor de g, que pasaría a ser g = g . ( µ . cos a + sen a )
B.-
Utilizando la tabla de equivalencia (se dan errores muy leves)
|
Pendiente |
µ = 0.2 |
µ = 0.4 |
µ = 0.6 |
µ = 0.8 |
µ = 1.0 |
|
12.5 % |
27 % |
14 % |
10 % |
7 % |
6 % |
|
6 % |
15 % |
7 % |
5 % |
4 % |
3 % |
|
3 % |
8 % |
4 % |
3 % |
2 % |
2 % |
El valor de µ arriba expresado implica un deslizamiento constante con el pavimento, pero bien puede suceder que el peatón voltee o gire con lo que habrá que introducir otro factor de corrección.
|
µ |
Corrección |
|
0,1 |
0,4 % |
|
0,2 |
1,5 % |
|
0,3 |
2,8 % |
|
0,4 |
3,9 % |
|
0,5 |
4,6 % |
|
0,6 |
4,9 % |
|
0,7 |
4,8 % |
|
0,8 |
4,3 % |
|
0,9 |
3,5 % |
|
1,0 |
2,5 % |
Lo último en el Foro de CausaDirecta.com
| Así ocurrió mi accidente | CALCULO DE LA VELOCIDAD DE MOTO | (7) |
| Luis H > 17/02/2025 | 07:30 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:13 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:12 | |
| Anécdotas | Milionário la calle | (3) |
| MIguelitoalc > 10/01/2025 | 12:27 | |
| Trámites y Reclamaciones | Accidente de moto. | (1) |
| Sègimer > 05/05/2024 | 09:03 | |
| Testigos de accidentes | Se buscan testigos accidente día 23/11/2023 en Valladolid | (2) |
| > 18/04/2024 | 19:07 | |
| Trámites y Reclamaciones | Discriminación en perfumeria Druni | (1) |
| Melior.Mundi > 03/03/2024 | 13:07 | |
| Así ocurrió mi accidente | Desconformidad y dudas en atestado Motocicleta | (1) |
| anteva2 > 24/11/2023 | 11:47 | |
| Punto de Encuentro (Investigación y Reconstrucción) | Documentación sobre la fórmula de Vangi-Cialdai | (1) |
| Jugo > 05/11/2023 | 22:04 | |
| Así ocurrió mi accidente | Dudas culpabilidad accidente, pref. derecha y exceso Velocid | (2) |
| pitutis > 12/10/2023 | 11:19 | |
Cálculos de velocidades y distancias para colisiones fronto-laterales
TakerCALCULO DE VELOCIDADES Y DISTANCIAS
Enviado por: Taker, y modificado el 09/11/03
1º OBTENCION DE DATOS
- Masas de vehículos (incluida la carga).
- Medidas de las huellas de frenada.
- Distancias alcanzadas tras la colisión.
- Ángulos de las posiciones finales de los vehículos.
2º DETERMINACION DE UN EJE DE COORDENADAS QUE SITUE LAS POSICIONES INICIALES, DE IMPACTO Y FINALES DE LOS VEHICULOS IMPLICADOS EN EL ACCIDENTE
Se procurará que el eje X pase por el centro de uno de los vehículos, para más adelante poder determinar las velocidades de colisión.
3º CALCULO DE LA VELOCIDAD A LA QUE SALEN DESPEDIDOS LOS VEHICULOS TRAS EL IMPACTO
V = v 2 . g . ( µ ± t ) . L
g es la gravedad, que vale 9,81 m/s².
µ es el coeficiente de rozamiento de las ruedas del vehículo con el pavimento.
t es la pendiente de la carretera y se expresa en tantos por uno, a sumar o restar a µ según que sea ascendente o descendente.
L es la distancia a la que queda el vehículo con respecto al punto de colisión.
4º CALCULO DE LA VELOCIDAD DE IMPACTO
Utilizaremos para ello la fórmula del Principio de la Conservación de la Cantidad de Movimiento Lineal:
M1 . V1 . cos a 1 (respecto del eje x) + M2 . V2 . cosa 2 (respecto del eje x) =
M1 . V1?. Cos a 1 (ángulo salida) ± M2 . V2?. Cos a 2 (ángulo salida) y,
± según que el ángulo de salida del vehículo 2 esté por encima del eje x o, por debajo.
Aquí cobra especial importancia el haber fijado el eje x por el centro geométrico del dibujo en planta del vehículo 1, de tal forma que, el cos a 1 (0º) es igual a 1 y, el cos a 2 (90º) es igual a 0, lo que simplifica la fórmula de arriba y permite despejar la velocidad inicial del vehículo 1 en función de las masas y velocidades finales.
Entonces:
V1 = M1 . V1?. Cos a 1 (ángulo salida) ± M2 . V2?. Cos a 2 (ángulo salida) / M1
M1 . V1 . sen a 1 (respecto del eje y) + M2 . V2 . sen a 2 (respecto del eje y) =
M1 . V1?. Sen a 1 (ángulo de salida) ± M2 . V2?. Sen a 2 (ángulo de salida)
Como sen a 1 (0º) es 0 y, sen a 2 (90º) es 1, tendremos que:
V2 = M1 . V1?. Sen a 1 (ángulo de salida) ± M2 . V2?. Sen a 2 (ángulo de salida) / M2
NOTA: Si el ángulo de entrada del vehículo 2 fuera distinto de 90º, por ejemplo 125º, la fórmula del PRINCIPIO DE LA CONSERVACION DE... sería:
M1 . V1 . cos a 1 (respecto del eje x)+M2 . V2 . cosa 2 (respecto del eje x)=
Ejemplo 0º ejemplo 125º
M1 . V1?. Cos a 1 (ángulo salida) ± M2 . V2?. Cos a 2 (ángulo salida)despejando:
V1 = M1 . V1?. Cos a 1 (ángulo salida) ± M2 . V2?. Cos a 2 (ángulo salida)-M2 . V2. Cos 125º / M1
Y:
M1 . V1 . sen a 1 (respecto del eje y) + M2 . V2 . sen a 2 (respecto del eje y) =
Ejemplo 0ºejemplo 125º
M1 . V1?. Sen a 1 (ángulo de salida) ± M2 . V2?. Sen a 2 (ángulo de salida) despejando:
V2 = M1 . V1?. Sen a 1 (ángulo de salida) ± M2 . V2?. Sen a 2 (ángulo de salida) /M2 . Sen 125º
Con el valor de V2 ya conocido lo sustituimos en V1 y ya lo tenemos.
5º CALCULO DE LA VELOCIDAD EN EL MOMENTO DE MARCAR LAS HUELLAS
V = v 2 . g . (µ ± t) . d + V (impacto)²
d es la distancia de la frenada.
6º CALCULO DE LA VELOCIDAD EN EL MOMENTO DEL BLOQUEO ( TIEMPO QUE TARDA EN MARCAR LAS HUELLAS)
Desde que las ruedas se bloquean y, hasta que por efecto del rozamiento, se calientan y desprenden material ? que queda pegado al pavimento formando la conocida huella de frenada- transcurre un tiempo. Tiempo en el que el vehículo pierde velocidad. Como se sabe que el espacio recorrido con ruedas bloqueadas sin dejar marcas, está entre el metro y los cuatro metros, se trata de averiguar la velocidad del móvil en el momento de bloquearse las ruedas. La fórmula, una vez más es:
V = v 2 . g. (µ ± t) . d + V (paso 5º)²
d es el espacio antes de dejar la marca ( 1 a 4 m).
7 º CALCULO DE LA VELOCIDAD EN EL MOMENTO DE PISARSE EL FRENO
PASO UNO (cálculo de la deceleración media que sufre el móvil al pisarse el freno y se bloquean las ruedas)
d = ½ µ . g
Conocido el valor medio de µ y usando la tabla de abajo, se determina el tiempo que tarda en bloquear las ruedas y la eficacia de la frenada.
|
DECELERACION |
TIEMPO DE ACTUACION |
EFICACIA FRENOS |
|
9,81 M/S² |
0,20 S |
100 % |
|
8,83 M/S² |
0,20 S |
90 % |
|
7,85 M/S² |
0,25 S |
80 % |
|
6,87 M/S² |
0,25 S |
70 % |
|
5,88 M/S² |
0,30 S |
60 % |
|
4,90 M/S² |
0,55 S |
50 % |
|
3,92 M/S² |
0,60 S |
40 % |
PASO DOS
V = V (anterior) + d. T
d es la deceleración media.
T es el tiempo de actuación deducido de la tabla.
8º CALCULO DE LA DISTANCIA QUE RECORRE DURANTE LA DECELERACION
e = V(inicial) . t ? ½ d . t²
9º CALCULO DEL ESPACIO RECORRIDO EN EL TIEMPO DE REACCION
e1 = V . t donde t = tiempo de reacción del conductor.
10º CALCULO DEL ESPACIO TOTAL RECORRIDO DESDE EL PUNTO DE PERCEPCION REAL
PPR = e + e1
Lo último en el Foro de CausaDirecta.com
| Así ocurrió mi accidente | CALCULO DE LA VELOCIDAD DE MOTO | (7) |
| Luis H > 17/02/2025 | 07:30 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:13 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:12 | |
| Anécdotas | Milionário la calle | (3) |
| MIguelitoalc > 10/01/2025 | 12:27 | |
| Trámites y Reclamaciones | Accidente de moto. | (1) |
| Sègimer > 05/05/2024 | 09:03 | |
| Testigos de accidentes | Se buscan testigos accidente día 23/11/2023 en Valladolid | (2) |
| > 18/04/2024 | 19:07 | |
| Trámites y Reclamaciones | Discriminación en perfumeria Druni | (1) |
| Melior.Mundi > 03/03/2024 | 13:07 | |
| Así ocurrió mi accidente | Desconformidad y dudas en atestado Motocicleta | (1) |
| anteva2 > 24/11/2023 | 11:47 | |
| Punto de Encuentro (Investigación y Reconstrucción) | Documentación sobre la fórmula de Vangi-Cialdai | (1) |
| Jugo > 05/11/2023 | 22:04 | |
| Así ocurrió mi accidente | Dudas culpabilidad accidente, pref. derecha y exceso Velocid | (2) |
| pitutis > 12/10/2023 | 11:19 | |
Determinación de la influencia de la velocidad excesiva en colisiones en intersección
Escrito por Luis-LopezDETERMINACIÓN DE LA INFLUENCIA DE LA VELOCIDAD EXCESIVA EN COLISIONES EN INTERSECCIÓN
Por Luis-Lopez
En colisiones en intersección suele ser habitual que la causa inmediata del accidente se encuentre en no respetar la prioridad de paso del vehículo que circula por la vía preferente por parte del conductor del vehículo que pretendía cruzar o incorporarse a la vía; pero también suele ser habitual, una vez determinada la velocidad inicial de cada uno de los vehículos, que el vehículo que circulaba por la vía preferente circulara a una velocidad excesiva con respecto a la limitación de la vía.
Esta circunstancia, ademas de incrementar los daños materiales y personales producidos, puede tener influencia en el desarrollo del accidente en el sentido que si el vehículo que circulaba a una velocidad excesiva hubiese circulado a la velocidad máxima permitida, las trayectorias de ambos vehículos no se hubiesen cruzado y por tanto no se habría producido el accidente, al haber cruzado ya la vía el vehículo que se incorporaba cuando el vehículo preferente no había llegado aún al punto de colisión, con la consiguiente redistribución de responsabilidades en la ocurrencia del accidente con respecto al caso de imputar la culpa del accidente únicamente al hecho de no respetar la prioridad por parte del conductor que se incorporaba. (Ej. responsabilidad: vehículo se incorpora 60/70%-vehículo preferente 40/30%).
Para tratar de determinar si pudiese darse la anterior circunstancia en un determinado caso se deberá realizar la siguiente serie de operaciones:
A.- Tras haber obtenido previamente la velocidad inicial y de colisión de ambos vehículos y existiendo un exceso sobre la norma de velocidad por parte del vehículo que circulaba por la vía preferente (en adelante vehículo B) se hallara primeramente el tiempo empleado por el vehículo que se incorporaba a la vía (en adelante vehículo A) desde el punto de entrada (habitualmente la línea transversal de STOP) hasta el punto de conflicto con la expresión
![]()
siendo T, el tiempo en segundos, S, el espacio recorrido y A, la aceleración máxima estimada para el vehículo que se incorporaba (Ver nota 1)
Ejemplo: El vehículo A penetró en la vía desde la posición de reposo (0 m/sg), en la línea de STOP, recorriendo un espacio de 9 metros hasta el punto de colisión con una aceleración máxima de 2,35 m/sg², obteniendo en tiempo de 2.76 sg.
B.- Seguidamente se obtendrá la situación del vehículo B con respecto al punto de colisión, en el momento que el vehículo A penetró en la vía, partiendo de la base que el tiempo empleado por el vehículo A en recorrer el espacio entre la línea de detención de STOP o punto de detención y el punto de colisión, es el mismo que el empleado por el vehículo B en recorrer el espacio comprendido entre la posición que ocupaba y el punto de colisión, es decir, el tiempo determinado en el apartado A, mediante la expresión
S = V T
siendo T, el tiempo hallado en el apartado A y V, la velocidad inicialmente hallada para ese vehículo.
Ejemplo: El vehículo B circulaba a 22,43 m/sg (80.74 km/h) siendo el tiempo empleado por el vehículo A de 2.76 sg, resultando estar, con la anterior operación, a 61.90 metros del punto de colisión cuando el vehículo A penetró en la vía.
C.- A continuación se determinara el tiempo que el vehículo A hubiese empleado en salir de la vía y por tanto de la posible trayectoria del vehículo B, momento que se daría cuando la parte posterior del vehículo A sobrepasara la línea del margen contrario de la vía, mediante idéntica expresión a la utilizada en el apartado A, siendo S, la distancia que debería recorrer el vehículo en cuestión mas la longitud total del mismo y A, la aceleración anteriormente determinada para ese vehículo.
Ejemplo: Debiendo recorrer el vehículo A 8.20 metros, mas 4.40 metros de su longitud, S tendría un valor de 12.60 metros y A de 2.35 m/sg², resultando un tiempo para dicho vehículo de 3.27 m/sg.
D.- Finalmente se determinara la distancia del vehículo B al punto de colisión, cuando el vehículo A hubiese salido de la vía, en el hipotético caso que el conductor del vehículo B hubiese respetado la limitación de velocidad, mediante la expresión
D = S - (T V)
siendo D, la distancia a determinar, S la distancia real del vehículo B al punto de colisión, cuando el vehículo A penetró en la vía, T el tiempo que el vehículo A hubiese necesitado para cruzar y salir de la vía y V la hipotética velocidad (m/sg) del vehículo B respetando la limitación de velocidad.
Ejemplo:
D = S - (T V)
D = 61.90 metros - ( 3.27 metros . 16.66 m/sg ) = 7.43 metros.
Es decir cuando la parte posterior del vehículo A hubiese cruzado la línea del arcén del margen izquierdo saliendo así de la vía, la parte frontal del vehículo B, circulando a la máxima velocidad permitida (60 km/h) estaría todavía a una distancia de 7.43 metros del Punto de Colisión, no produciendose así la misma.
Nota 1: Inicialmente la aceleración máxima disponible esta en función del coeficiente de adherencia estimado (µ) para un determinado vehículo y el valor de la gravedad (g), con arreglo a la expresión (a = µ.g).
Así mismo se puede determinar el valor máximo de aceleración para un determinado vehículo, con arreglo a los datos técnicos publicados por el fabricante, habitualmente en forma de tiempo empleado en pasar de 0 a 100 km/h, utilizando la siguiente expresión del movimiento uniformemente acelerado
V.final (m/sg)- V.inicial (m/sg)
Aceleración (m/sg²) = ---------------------------------------
Tiempo(sg)
Ahora bien los valores de aceleración máxima obtenidos por cualquiera de ambos sistemas deben modificarse ligeramente antes de su utilización en otras formulaciones, puesto que dichos valores son los conseguidos por un piloto muy experimentado y en condiciones de prueba, siendo la aceleración en condiciones de conducción normal del orden del 70 % de la máxima posible.
Nota 2: La formulación utilizada en los apartados A y C del presente se utilizaran en el supuesto que el vehículo inicie su movimiento desde la posición de reposo (V.inicial = 0 m/sg-movimiento uniformente acelerado)
En el caso de no ser así se deberá determinar si el movimiento descrito era uniformemente acelerado/decelerado (con velocidad inicial) o uniforme (velocidad constante), utilizando entonces, las fórmulas que relacionan espacio, tiempo y/o aceleración en esos movimientos.
Lo último en el Foro de CausaDirecta.com
| Así ocurrió mi accidente | CALCULO DE LA VELOCIDAD DE MOTO | (7) |
| Luis H > 17/02/2025 | 07:30 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:13 | |
| Testigos de accidentes | BUSCO TESTIGOS ACCIDENTE TUNEL SANTA COLOMA 20/12/24 | (1) |
| olga70 > 06/02/2025 | 13:12 | |
| Anécdotas | Milionário la calle | (3) |
| MIguelitoalc > 10/01/2025 | 12:27 | |
| Trámites y Reclamaciones | Accidente de moto. | (1) |
| Sègimer > 05/05/2024 | 09:03 | |
| Testigos de accidentes | Se buscan testigos accidente día 23/11/2023 en Valladolid | (2) |
| > 18/04/2024 | 19:07 | |
| Trámites y Reclamaciones | Discriminación en perfumeria Druni | (1) |
| Melior.Mundi > 03/03/2024 | 13:07 | |
| Así ocurrió mi accidente | Desconformidad y dudas en atestado Motocicleta | (1) |
| anteva2 > 24/11/2023 | 11:47 | |
| Punto de Encuentro (Investigación y Reconstrucción) | Documentación sobre la fórmula de Vangi-Cialdai | (1) |
| Jugo > 05/11/2023 | 22:04 | |
| Así ocurrió mi accidente | Dudas culpabilidad accidente, pref. derecha y exceso Velocid | (2) |
| pitutis > 12/10/2023 | 11:19 | |
